Analyzing representational similarity among neural networks (NNs) is essential for interpreting or transferring deep models. In application scenarios where numerous NN models are learned, it becomes crucial to assess model similarities in computationally efficient ways.
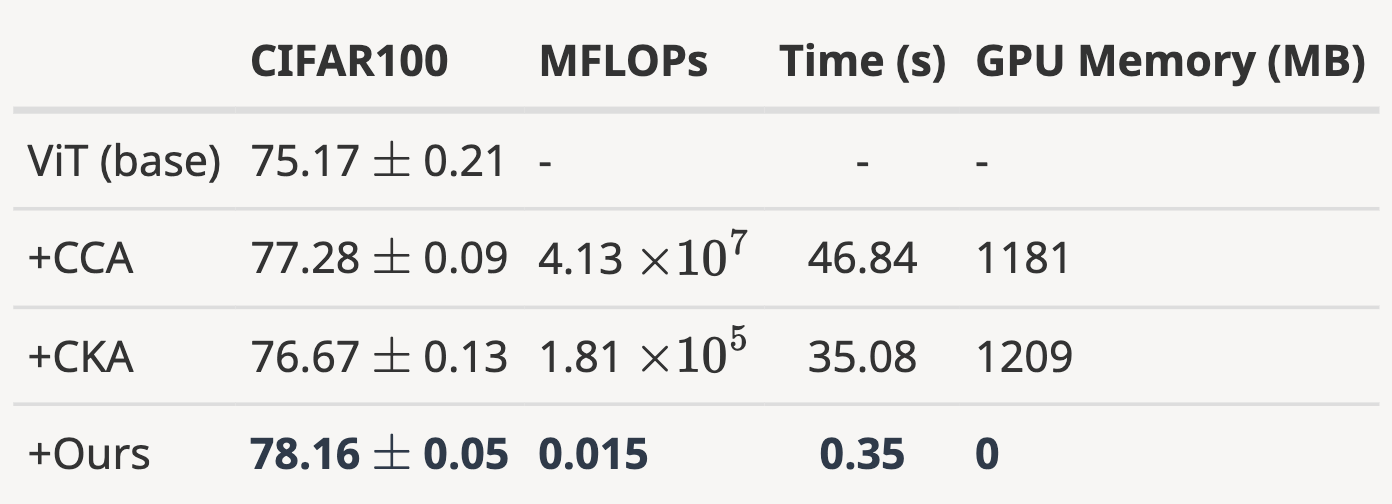
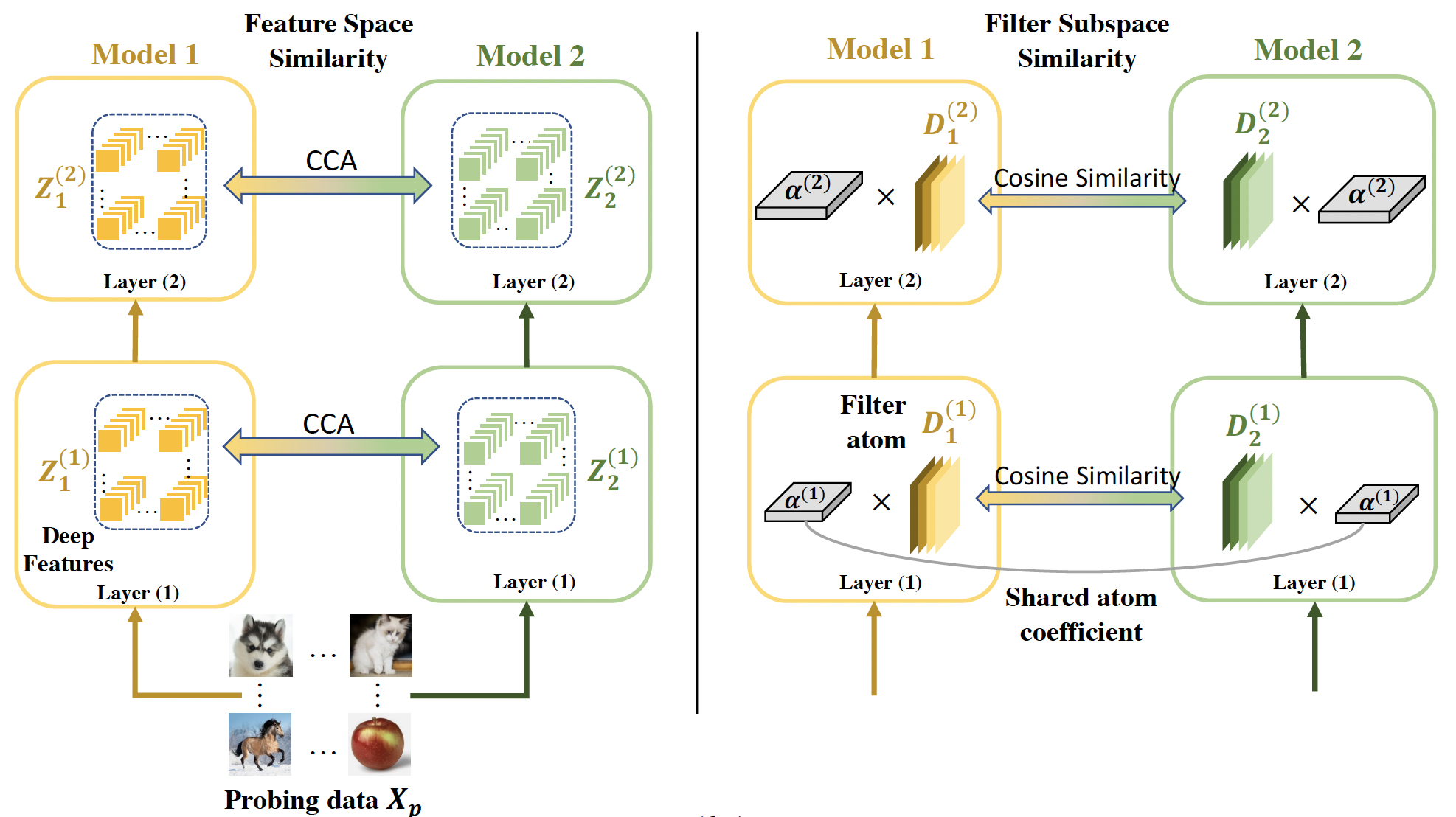
In this paper, we propose a new paradigm for reducing NN representational similarity to filter subspace distance. 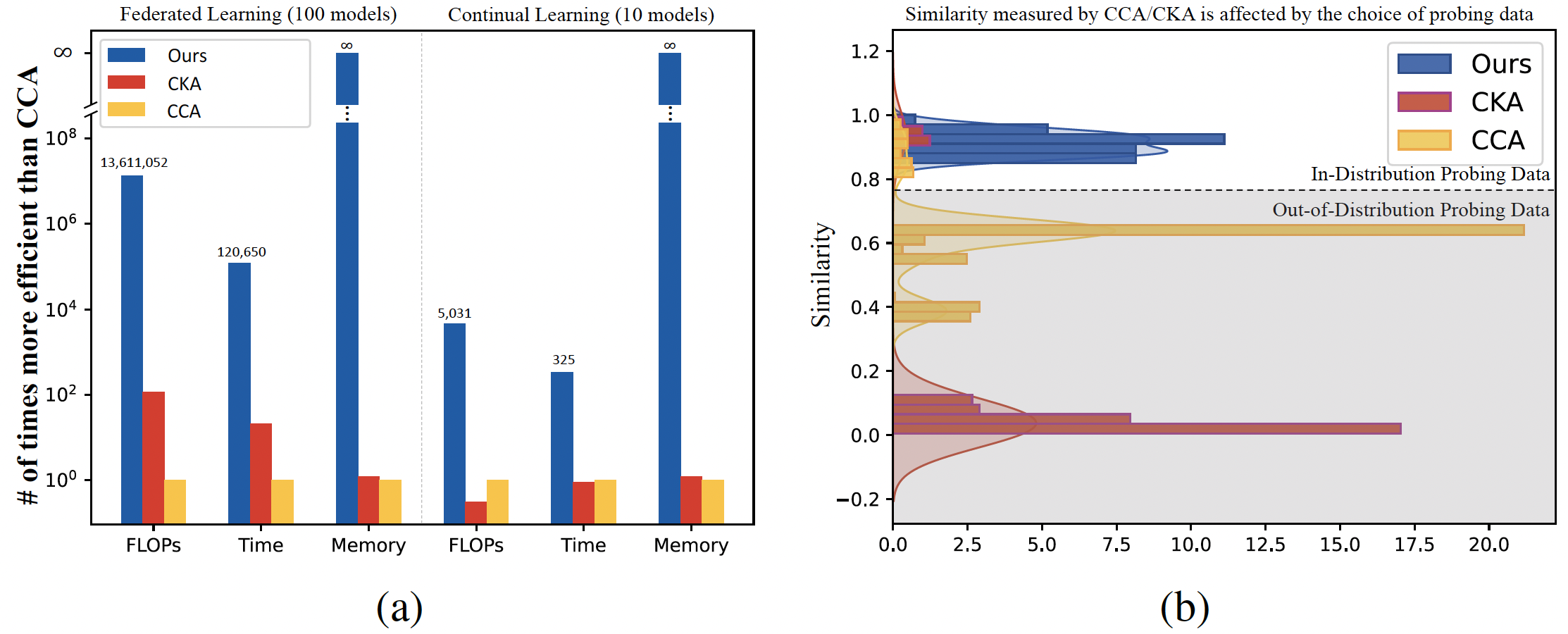Specifically, when convolutional filters are decomposed as a linear combination of a set of filter subspace elements, denoted as filter atoms, and have those decomposed atom coefficients shared across networks, NN representational similarity can be significantly simplified as calculating the cosine distance among respective filter atoms, to achieve millions of times computation reduction over popular probing-based methods.
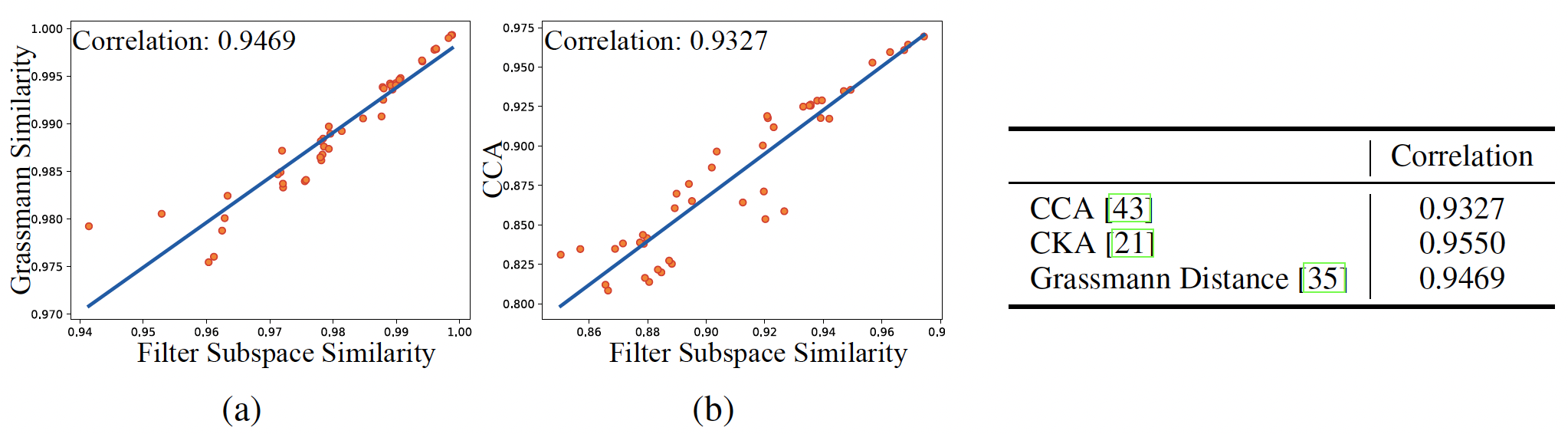
We provide both theoretical and empirical evidence that such simplified filter subspace-based similarity preserves a strong linear correlation with other popular probing-based metrics, while being significantly more efficient to obtain and robust to probing data. We further validate the effectiveness of the proposed method in various application scenarios where numerous models exist, such as federated and continual learning as well as analyzing training dynamics. We hope our findings can help further explorations of real-time large-scale representational similarity analysis in neural networks.
Filter subspace-based representational similarity: (1) Represent convolutional filters w as filter atoms D (filter subspace elements) and atom coefficients α. (2) Calculates the filter subspace similarity between a small portion of parameters, i.e., filter atoms.
(a) The ratio of the computational cost savings of our filter subspace similarity over probing-based similarities. (b) Out-of-distribution data have negative impact on probing-based similarity, while no impact on our filter subspace similarity since it does not rely on probing data.
Our filter subspace similarity shows strong correlation with (a) Grassmann similarity and (b) CCA.
Classification accuracy of model ensemble using different FL methods and model selection strategies: Models are selected with different similarity measures in each setting. The model ensemble using our filter subspace-based method is millions of times faster and consumes much fewer resources than probing-based methods while producing comparable performance.
Continual Learning Results. The model ensemble using our filter subspace similarity is significantly faster and consumes much fewer resources than probing-based methods, while maintaining comparable classification accuracy.
Continual Learning Results with ViT. Although our method focuses on convolutional filter subspace due to the highly compact size of resulting filter subspace elements (atoms), it can also be easily extended to other types of layers, e.g., linear layers.
In this paper, we proposed a new paradigm for reducing representational similarity analysis in CNNs to filter subspace distance assessment, which is targeted for application scenarios where numerous models are learned. We provided both theoretical and empirical evidence that the proposed filter subspace-based similarity exhibits a strong linear correlation with popular probing-based metrics while being significantly more efficient and robust in probing data.